The factor by which phenomena on the surface of the earth are reduced in order to be shown on a map

Methods of repesenting scale;

• Statement of scale e.g. 1 cm represents 10 km
• Representative fraction (R.F) e.g. 1:50000
• Graphical or bar scale

It's frameworks used to determine position on the surface of the earth

For example, Geographic coordinate system (GCS);

• A 3D coordinate system commonly used to define locations on the earth's surface
• Latitude is measured relative to the equator at 0 degree, with maxima of either 90 degrees north at the North Pole or 90 degrees south at the South Pole
• Longitude is measured relative to the prime meridian at 0 degree, with maxima of 180 degrees west or 180 degrees east

A mathematical expression used to transform locations from a 3D, spherical coordinate system to a 2D planar system

Map projection is done at a chosen scale

Why do we need map projection (problems with globes)?

• Globe isn't very portable
• Globe small scale makes them of limited practical use (i.e., geographic detail is sacrificed)

The 3 surfaces used for map projections: Cone, Cylinder, & Plane.

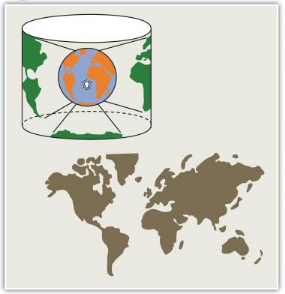
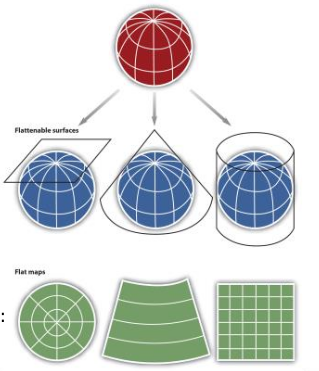
Transforming from 3D surface of the earth to a 2D plane, distortions are not only introduced but also inevitable

Distortions

• distance, direction, & area

Map projections

• Equidistant
• Conformal
• Equal area or equivalent

Preserve the quality of area

Used when accurate measures or comparisons of geographical distributions are necessary (e.g., deforestation, wetlands)

In an effort to maintain true proportions in the surface of the earth, features sometimes become compressed or stretched depending on the orientation of the projection

Moreover, such projections distort distances as well as angular relationships

Represent angles correctly between locations, also referred to as bearings

Used for navigational purposes due to the importance of maintaining a bearing or heading when traveling great distances

• The cost of preserving bearings is that areas tend to be quite distorted in conformal map projections
• Though shapes are more or less preserved over small areas, at small scales areas become wildly distorted

The Mercator projection is an example of a conformal projection and is famous for distorting Greenland

Accurately represent distances

• Note that distances are only correct in one direction, usually running north-south, and are not correct everywhere across the map

Used for small-scale maps that cover large areas because they are good for preserving the shape of geographic features such as continents

Queries about this Lesson, please send them to: jmwaura.uni@gmail.com

*References*

• Mapping, Society, and Technology, Steven Manson
• Web Cartography, Map Design for Interactive and Mobile Devices, Ian Muehlenhaus
• Web Cartography, Menno-Jan Kraak and Allan Brown, ITC
• Cartography, Thematic Map Design, Borden D. Dent
• GIS Cartography, A Guide to Effective Map Design, Gretchen N. Peterson
• Thematic Cartography and Geovisualization, Terry A. Slocum et.al